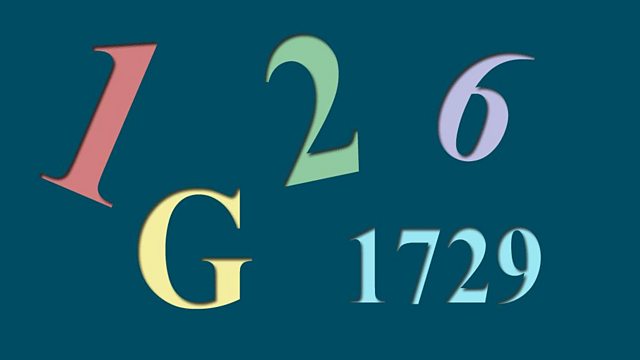麻豆约拍

Curious properties sometimes lurk within seemingly undistinguished numbers. 1729 sparked one of maths most famous anecdotes: a young Indian, Srinivasa Ramanujan, lay dying of TB in a London hospital. G.H. Hardy, the leading mathematician in England, visited him there. 'I came over in cab number 1729,' Hardy told Ramanujan. 'That seems a rather dull number to me.'

'Oh, no!' Ramanujan exclaimed. '1729 is the smallest number you can write as the sum of two cubes, in two different ways.' Most of us would use a computer to figure out that 1鲁 + 12鲁 = 9鲁 + 10鲁 = 1729. Ramanujan did it from his sickbed without blinking.

Mathematicians have mined his theorems ever since. In the last in the current series Simon Singh examines their impact and how mathematicians have proved them and put them to use. Far more than just another number theory, 1729 is the first of the 'Ramanujan numbers' or taxicab numbers. Mathematicians are competing to search for more of them (with higher powers) and testing the strength of new computing technology. The search is seen as mathematics' current greatest challenge. Only recently, a lost bundle of Ramanujan's notebooks turned up in a Cambridge library setting maths off on a new voyage of discovery.